B. Formulas and Derivations

For completeness, we give here the rest of the formulas not given throughout the paper, and the derivations of those not found in the literature.

B..1 Density Functions

• standard normal distribution [16]:

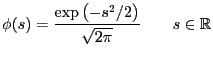  $$\phi(s) = \frac{\exp\left( -s^2 / 2 \right)}{\sqrt{2 \pi}} \qquad s \in \mathbb{R}$$ (18)

  
  

• exponential distribution [16]

  $$\psi(s;\lambda) = \lambda \exp(-\lambda s) \qquad \lambda>0,\,s \ge 0$$ (19)

  
  

B..2 Cumulative Distribution Functions

• standard normal [16]:

  $$\Phi(s) = \frac{1}{2} \left[ 1 + \mathrm{erf}\left(\frac{s}{\sqrt{2}}\right) \right] \qquad s \in \mathbb{R}$$ (20)

  
  
  where $\mathrm{erf}(.)$ is the error function.

• two-side truncated normal [10, pp.156-162]:

  $$F(s\vert 1) = \frac{\Phi\left( \frac{s-\mu}{\sigma} \right) - \Phi(\alpha) } {\Phi(\beta) - \Phi(\alpha) } \quad s \in [s_{\min}, s_{\max}]$$ (21)

  
  
  where $\alpha$ and $\beta$ are given by Equation 11.

• exponential [16]:

  $$\Psi(s;\lambda) = 1- \exp(-\lambda s) \qquad s \ge 0$$ (22)

  
  

• shifted and right-truncated exponential:

  $$F(s\vert) = \frac{\Psi(s-s_{\min};\lambda)}{\Psi(s_{\max}-s_{\min};\lambda)} \quad s \in [s_{\min}, s_{\max}]$$ (23)

  
  

B..3 Moments of a Truncated Normal

These can be found in the literature, e.g. in [10]. Let $S$ be a normally-distributed random variable with mean $\mu$ and variance $\sigma^2$ , which we left-truncate at $s_{\min}$ and right-truncate at $s_{\max}$ .

B..3.1 Expected Value

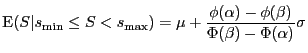$$\mathrm{E}(S\vert s_{\min} \le S < s_{\max}) = \mu + \frac{\phi(\alpha) - \phi(\beta) } {\Phi( \beta ) - \Phi( \alpha) } \sigma$$ (24)

We do not us the $\le$ sign at the upper limit of $S$ here (and in the equations below) to denote that the right-truncation is an option (i.e. $s_{\max}$ can be $+\infty$ ) in the context of this paper.

B..3.2 Variance

$$\mathrm{V}(S\vert s_{\min} \le S < s_{\max}) =$$

$$= \sigma^2 \left[ 1 + \frac{\alpha\,\phi(\alpha) - \beta\,\phi(\b... ...frac{\phi(\alpha) - \phi(\beta)} {\Phi(\beta) - \Phi(\alpha)} \right)^2 \right]$$ (25)

B..4 Moments of a Shifted Truncated Exponential

We have not found those in the literature. Let 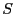$S$ be an exponentially distributed random variable with rate parameter $\lambda$ , which we shift by $s_{\min}$ and right-truncate at $s_{\max}$ .

B..4.1 Expected Value

From the definition of the expected value of a truncated distribution⁸and Equation 19

$$\mathrm{E}(S\vert s_{\min} \le S < s_{\max}) = \frac{ \int_{s_{\m... ...\, \psi(s-s_{\min};\lambda) \, \mathrm{d}s} {\Psi(s_{\max}-s_{\min};\lambda)} =$$

$$= \frac{\lambda \exp( \lambda s_{\min})} {\Psi(s_{\max}-s_{\min};\lambda)} \int_{s_{\min}}^{s_{\max}} s \exp(-\lambda s ) \, \mathrm{d}s$$

where the shift of the exponential by $s_{\min}$ is already taken into account. From lists of integrals of exponential functions⁹

$$\int_{s_{\min}}^{s_{\max}} s \exp(-\lambda s ) \, \mathrm{d}s = \... ...s)}{-\lambda} \left(s - \frac{1}{-\lambda}\right) \right]_{s_{\min}}^{s_{\max}}$$

Putting the last 2 equations together and working out the calculation leads to

$$\mathrm{E}(S\vert s_{\min} \le S < s_{\max}) = \frac{1}{\lambda} ... ...in} } { \Psi(s_{\max} -s_{\min};\lambda) } % = \left(\frac{1}{\lambda}\right)$$ (26)

For only shift but no truncation ( $s_{\min} \ne 0$ , $s_{\max} = +\infty$ ), $\psi(s_{\max}-s_{\min};\lambda) = 0$ and $\Psi(s_{\max} -s_{\min};\lambda) = 1$ , so Equation 26 becomes

$$\mathrm{E}(S\vert s_{\min} \le S) = \frac{1}{\lambda} + s_{\min}$$

which for a zero shift ( 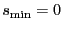$s_{\min} = 0$ ) it becomes $\mathrm{E}(S) = 1/\lambda$ , as expected [16].

B..4.2 Variance

We can break down a shifted $S$ to a mixture of its right-truncated and left-truncated parts weighted by $a$ and $b$ where $a+b = 1$ . The two parts are non-correlated, so for their variances it holds that

$$\mathrm{V}(S\vert s_{\min} \le S) = \nonumber a^2 \mathrm{V}(S \vert s_{\min} \le S < s_{\max} ) + b^2 \mathrm{V}(S\vert s_{\max} \le S) \nonumber$$

$$\Rightarrow \mathrm{V}(S \vert s_{\min} \le S < s_{\max}) = \frac{\mathrm{V}(s_{\min} \le S) - b^2 \mathrm{V}(S\vert s_{\max} \le S)}{a^2 }$$

Since shifts do not affect variances, $\mathrm{V}(S\vert s_{\min} \le S) = \mathrm{V}(S\vert s_{\max} \le S) = 1/\lambda^2$ . Moreover, $a = \Psi(s_{\max}-s_{\min})$ , leading to

$$\mathrm{V}(S\vert s_{\min} \le S < s_{\max}) = \frac{1}{\lambda^2} \left( \frac{2}{ 1- \exp( \lambda ( s_{\min}-s_{\max} ) ) } - 1 \right)$$ (27)

For only shift but no truncation ( 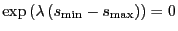$s_{\min} \ne 0$ , $s_{\max} = +\infty$ ), $\exp\left(\lambda\left( s_{\min} - s_{\max} \right)\right) = 0$ and Equation 27 becomes

$$\mathrm{V}(S\vert s_{\min} \le S) = \frac{1}{\lambda^2} = \mathrm{V}(S)$$

as expected; the shift does not affect the variance [16].

Footnotes

... distribution⁸

http://en.wikipedia.org/wiki/Truncated_distribution

... functions⁹

http://en.wikipedia.org/wiki/List_of_integrals_of_exponential_functions